Джим Кокс (Великобритания), перевод Артёма Терейковского
В заключительной части статьи рассматриваются магнитные характеристики различных марок распылённого железа от компании Micrometals, а также специфические аспекты применения сердечников из этого материала в сглаживающих дросселях, сетевых фильтрах и других индуктивных компонентах.
Предыдущие статьи: часть 1, часть 2.
Переменная составляющая тока в обмотке дросселя постоянного тока способна значительно влиять на потери в сердечнике и на параметры индуктивности из-за изменений начальной магнитной проницаемости используемых материалов. Графики, которые можно увидеть на рис. 2, были получены при условии, что амплитуда магнитной индукции не превышает 1 мТл, что, как правило, соответствует менее чем 1% от переменной составляющей тока в обмотке. На рис. 3 изображена зависимость потерь материала -52 от амплитуды индукции переменного магнитного поля в сердечнике.
В изготовлении дросселей для выходных фильтров импульсных источников питания наиболее часто применяется материал -26. Однако с увеличением частоты рекомендуется использовать материалы -8, -18 и -52, которые обладают меньшими потерями.
Максимальные уровни индукции переменного тока в тороидальных сердцах дросселей фильтров, расположенных на выходе импульсных источников вторичного питания (ИВЭП), во время функционирования не превышают 1000 Гс, при этом типичное значение составляет около 200 Гс. Влияние амплитуды магнитной индукции на магнитную проницаемость различных материалов представлено на рисунке 8. Для большинства материалов наблюдается заметное увеличение магнитной проницаемости при амплитуде индукции, превышающей 100 Гс. Наивысший прирост зафиксирован у материалов с высокой начальной проницаемостью, таких как -26, -40, -45 и -52.
Рисунок 9 демонстрирует зависимость начальной магнитной проницаемости от совокупной напряженности магнитного поля для материала -26 при различных значениях пульсаций в обмотках. Похожие зависимости были установлены для материалов -40 и -52.
Рассмотрим несколько примеров.
ДРОССЕЛИ С ПОДМАГНИЧИВАНИЕМ ПОСТОЯННЫМ ТОКОМ
Пример 1
Исходные условия. Требуется выполнить расчёт дросселя, индуктивность (L) которого должна быть равна 45 мкГн при подмагничивании постоянным током (I) 7,5 А. При этом уровень пульсаций должен оставаться в пределах 1%. В ходе проектирования необходимо оптимизировать конструкцию дросселя, прежде всего учитывая его стоимость, а также нагрев в процессе работы. Важно также стремиться к сокращению габаритов дросселя, насколько это возможно.
Выполнение задания. На первом этапе требуется выбрать материал для дросселя. В первую очередь целесообразно рассмотреть смеси -26, -40 и -52 как наиболее экономичные, так как в условиях задачи нет требований относительно изменения индуктивности дросселя при варьировании тока в обмотке.
Энергия, запасаемая в дросселе, составит:
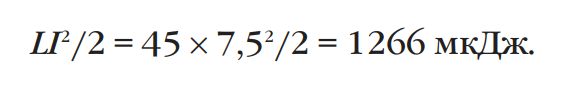
Следующий этап заключается в выборе размера и формы сердечника. В данном случае идеально подойдет материал -52. Использование кольца Т106 позволит ограничиться однослойной обмоткой при температурном повышении менее 25°C (см. рис. 2).
Определение количества витков осуществляется следующим образом. Согласно кривым, представленным в верхней части рисунка 2, для того чтобы накопить 1266 мкДж в сердечнике Т106-52, потребуется примерно 200 Ампер-витков. Таким образом, количество витков обмотки составит:
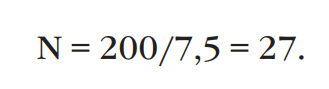
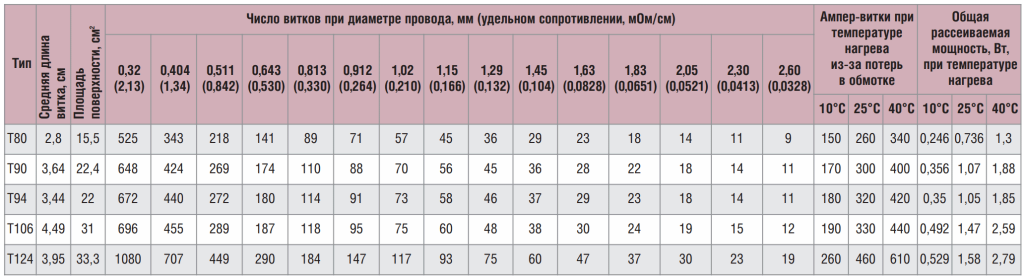
Согласно таблице 4, выбираем однослойную обмотку с проводом диаметром 1,15 мм. Этот выбор гарантирует, что перегрев не превысит 25°C.
Пример 2
Исходные требования. Необходимо провести расчёт дросселя с индуктивностью (L) 60 мкГн без подмагничивания и 45 мкГн при постоянном токе (I) 7,5 А. При этом следует обеспечить, чтобы степень насыщения сердечника оставалась ниже 25%, а пульсации не превышали 1%. В процессе расчёта нужно оптимизировать конструкцию дросселя, уделяя внимание прежде всего его размерам, а также нагреву во время работы. Также следует стремиться к снижению стоимости дросселя.
Реализация задания. В первую очередь необходимо выбрать материал для дросселя. Наилучшие варианты – это смеси -8, -18, -28 и -33, так как они обладают низкой амплитудной нелинейностью проницаемости. Из-за ограниченности изменения индуктивности в пределах рабочих токов эти материалы в данной ситуации будут наиболее подходящими.
Энергия, накапливаемая в дросселе, будет равна 1266 мкДж, как и в первом примере.
Следующим этапом является выбор параметров сердечника. Исследование графиков для различных материалов демонстрирует, что использование смеси -8 в качестве сердечника позволит создать кольцо минимальных размеров (см. рис. 6). Сердечник Т94-8 гарантирует, что температура не превысит 40°C при «полной» намотке. Согласно графику в нижней части рисунка 6, при накоплении 1266 мкДж сердечник Т94-8 работает с уровнем насыщения примерно 15%, что полностью соответствует заданным условиям.
Для вычисления числа витков (N) применим следующую формулу:
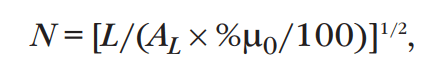
где AL – площадь сердечника (см^2), %μ0 – доля начальной проницаемости.
После замены значений мы получаем:
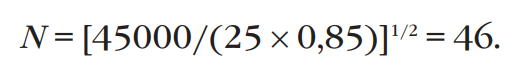
Для того чтобы обеспечить нагрев кольца Т94 до показателя менее 40°C, необходимо использовать «полную» намотку, что отражено в таблице 10. Оптимальный диаметр провода составляет 1,29 мм.
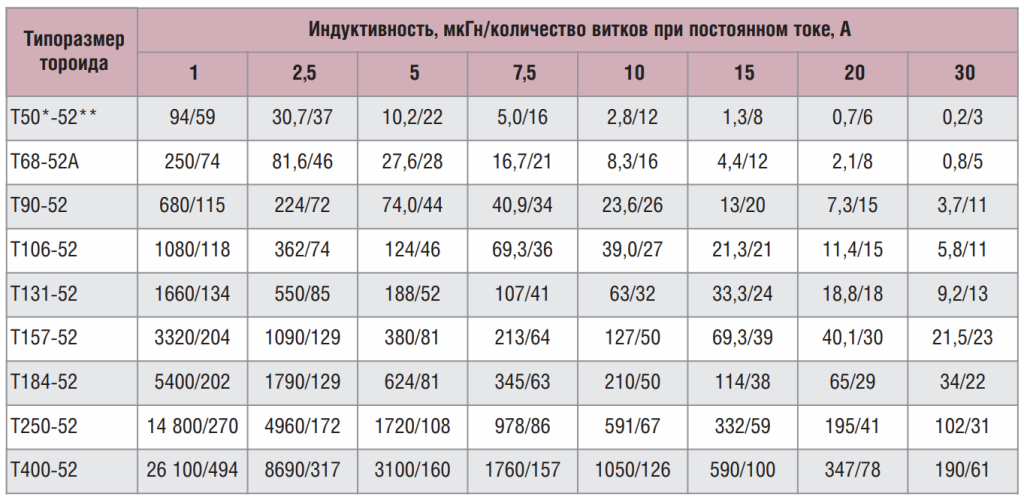
Для расчета количества витков, основываясь на индуктивности и максимально допустимом постоянном токе в обмотке для сердечников из смеси -52, можно обратиться к таблице 11. Данные, приведенные в этой таблице, предполагают уровень пульсаций ниже 1% и температурный предел в 40°C, учитывая потери, возникающие в обмотке и сердечнике. Значительные пульсации могут привести к увеличению температуры и индуктивности дросселя. Чтобы определить диаметр провода в зависимости от максимального постоянного тока, стоит воспользоваться таблицей 12.

ДРОССЕЛИ ПЕРЕМЕННОГО ТОКА
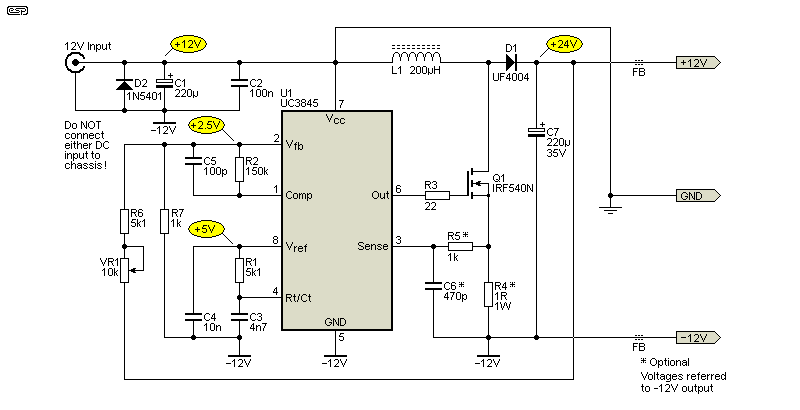
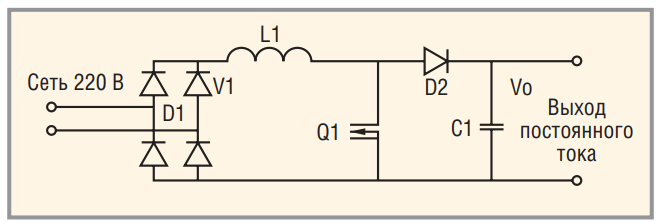
В последнее время возросли требования к сокращению гармоник тока, который блок ИВЭП потребляет от сети 220/380 В. Для достижения этой цели даже в источниках питания с относительно низкой мощностью начали внедрять активные корректооры коэффициента мощности (ККМ). Схема, иллюстрирующая структуру стандартного блока ККМ, представлена на рис. 14.
Корректор коэффициента мощности (ККМ) отличается от стандартного импульсного преобразователя тем, что на его входе имеется выпрямленное, но не сглаженное сетевое напряжение. Управляющая логика ККМ (не показана на рисунке) должна организовать такой режим работы ключа Q1, чтобы вход преобразователя воспринимался как активное сопротивление. При этом между сетевым напряжением и текущим потреблением отсутствует фазовый сдвиг (cos ϕ = 1). В то же время, на выходном конденсаторе поддерживается стабильное напряжение, относительно мало зависящее от нагрузки и сетевого напряжения. Расчет потерь в сердечнике дросселя такого преобразователя более сложен, чем в ранее упомянутых случаях, поскольку магнитный поток в сердечнике постоянно меняется на протяжении полупериода питающего напряжения даже при фиксированном входном напряжении и стабильной нагрузке.
Предлагаемый ниже метод основан на использовании синусоидального входного напряжения, стабильного выходного напряжения и постоянной частоты преобразования ключевых компонентов, которая не зависит от управления этими компонентами.
Амплитудное значение индукции в магнитопроводе вычисляется, опираясь на форму напряжения, подаваемого на дроссель, согласно следующей формуле:
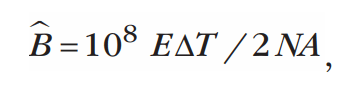
где E – максимальное значение напряжения на дросселе (В), ΔT – временной интервал (с), N – количество витков обмотки, A – площадь поперечного сечения сердечника (см²).
Максимальное значение Bmax достигается при Vi = Vo/2, где Vi – текущее значение входного напряжения, Vo – постоянное значение выходного напряжения.
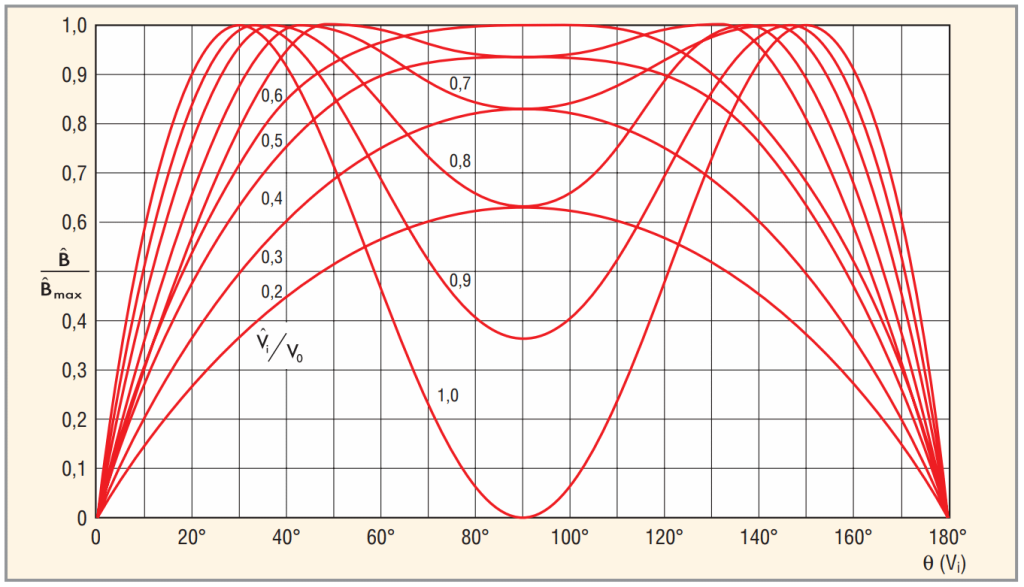
График зависимости отношения B/Bmax от фазы входного напряжения для различных соотношений Vi/Vo представлен на рисунке 15.
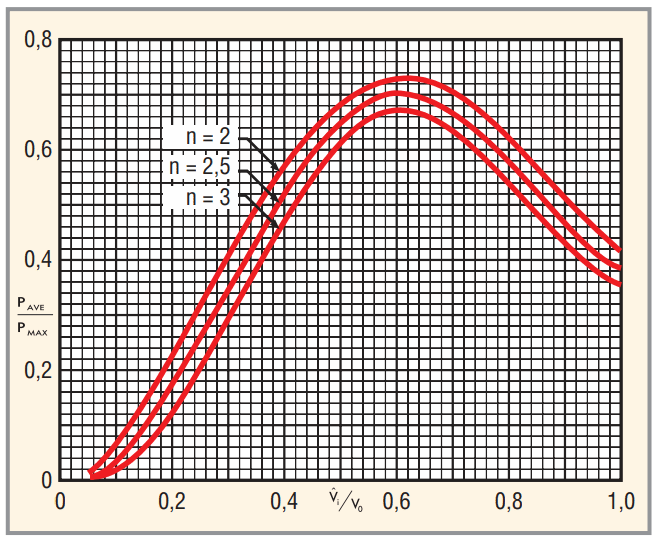
При заданной частоте преобразования потери в сердечнике пропорциональны Bn, где n варьируется от 1,65 до 3,00 для большинства порошковых материалов, включая распылённое железо. На рисунке 16 показано соотношение средней величины потерь к максимальному значению (при Vi = Vo/2) за полупериод питающего напряжения для значений n равных 2,0, 2,5 и 3,0.
С графика можно увидеть, что максимальное значение соотношения средних потерь к максимальным наблюдается при коэффициенте амплитудного входного напряжения к постоянному выходному напряжению, равном примерно 0,61. В то же время соотношение потерь меняется незначительно: от 0,672 при n = 3 до 0,725 при n = 2.
Поскольку подавляющее большинство контрольно-кассовых машин работает на уровне потерь, приближенном к максимальной величине, при их проектировании рекомендуется применять эмпирическое правило, согласно которому в наихудшем сценарии средний уровень потерь составляет 70% от значения, установленного при Vi = Vo/2. Амплитуда индукции в сердечнике вычисляется по следующей формуле:
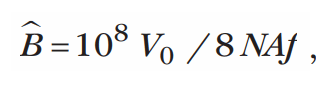
где f – частота переключения преобразователя.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПРЕДЕЛЕНИЯ ПОТЕРЬ
Изготовители магнитных веществ зачастую используют формулу Штейнмеца для расчета потерь в магнитных сердечниках:
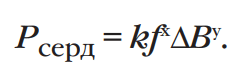
В данной формуле потери указаны в мВт/см3, частота – в кГц, а индукция в сердечнике – в теслах (Тл). Коэффициенты Штейнмеца k, x и y выбираются для достижения наилучшего соответствия с измеренными данными. Однако, к сожалению, применение этого уравнения дает правильные результаты лишь в определенных пределах рабочей частоты и плотности магнитного потока в сердечнике. Поэтому производители часто предлагают несколько наборов коэффициентов для различных диапазонов. Тем не менее, как указано в статье [1], это может привести к значительным расхождениям при расчетах потерь на границах этих диапазонов.
Общие потери в сердечнике представляют собой сумму потерь на перемагничивание и на вихревые токи. Потери на вихревые токи пропорциональны квадрату амплитудного значения магнитного потока и квадрату рабочей частоты. В то время как потери на перемагничивание линейно зависят от частоты, соотношение между компонентами потерь изменяется в зависимости от плотности магнитного потока и материала сердечника.
В работе Бозорта [2] было установлено, что потери на перемагничивание для дисперсного железа зависят от индукции, пропорционально B^3 при низких значениях и B^1,6 при высоких. При изменении индукции коэффициент изменяется в диапазоне от 1,6 до 3. Динамика этих изменений определяется тем, как стенки магнитных доменов реагируют на внешнее магнитное поле. В условиях слабых магнитных полей стенки доменов смещаются, оставаясь при этом «прикреплёнными» к различным дефектам кристаллической решётки. С увеличением напряженности поля растёт энергия доменов, что приводит к резкому преодолению дефектов в решётке. В условиях сильных магнитных полей материал выходит на уровень насыщения: диполи выстраиваются вдоль линий силового поля, и дальнейшее увеличение намагниченности не наблюдается.
Если принимать во внимание, что потери на перемагничивание ограничены тремя прямыми линиями (смотрите верхнюю часть рисунка 17), кривая потерь может быть определена как обратная сумма обратных значений уравнений, описывающих эти прямые:
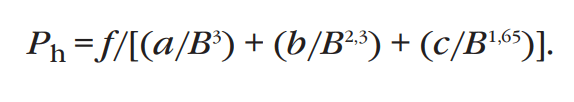
Потери на вихревые токи определяются по формуле:
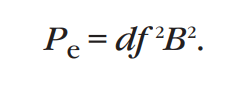
Следовательно, совокупные потери в сердечнике составят:
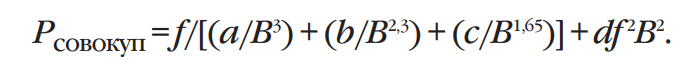
Модель, представленная в данном уравнении, называется моделью Оливера. Для достижения максимальных значений индукции было выбрано значение экспоненты 1,65 вместо 1,6, так как оно наиболее точно подходит для распылённого железа. Экспоненты для минимальных и промежуточных значений индукции также оптимизированы для всех видов распылённого железа, производимого компанией Micrometals. Изменяются лишь значения коэффициентов a, b и c.
В нижней части рисунка 17 показаны кривые потерь на перемагничивание, потерь, связанных с вихревыми токами, а также общие потери смеси 52 при частоте 100 кГц.
Было осуществлено исследование потерь, полученных в результате измерений на примере кольца Т106-52, и их сравнение с потерями, вычисленными по уравнениям Штейнмеца и Оливера в диапазоне частот от 60 Гц до 500 кГц. Результаты показали, что средняя ошибка, связанная с моделью Оливера, составляет не более 4,9%. В расчетах коэффициенты для уравнения Оливера были выбраны из таблицы 13. В свою очередь, средняя ошибка модели Штейнмеца достигает 20%. Наибольшие ошибки возникают при небольших значениях индукции и потерях в сердечнике, так как данная модель была изначально настроена на потери выше 10 мВт/см^3.
Модель Оливера обладает большей точностью, что позволяет точно определить вклад каждой составляющей в общие потери и произвести расчеты индуктивных элементов, функционирующих на предельных режимах, с достаточной степенью точности.
Как показано на рисунке 17, соотношение между различными компонентами потерь варьируется в зависимости от уровня индукции в сердечнике при фиксированной частоте. Примечательно, что при низких значениях индукции потери из-за вихревых токов становятся доминирующими. Если мы можем провести экстраполяцию на очень низкие значения индукции, это позволит нам точно определить коэффициенты в модели Оливера. Для этого необходимо провести измерение коэффициента Q с использованием высокоточного LCR-измерителя. Реальные потери в сердечнике можно вычислить по следующей формуле:
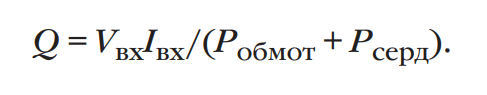
Когда измерения коэффициента Q проводятся на достаточно высоких частотах при низких значениях индукции, где заметно преобладают потери на вихревые токи, возможно вычислить коэффициент d для модели Оливера.
В данном случае используется сердечник Т106-52 с 100 витками обмотки. Индукция в этом сердечнике ограничена 0,01 мТл, а сопротивление обмотки на частоте 100 кГц составляет 0,74 Ом. При входном напряжении Vвх = 29 мВ, входном токе Iвх = 0,049 мА и коэффициенте Q = 45,5, потери в сердечнике составляют 2,99 × 10^(–8) Вт. Преобразовывая эти потери в удельное значение в мВт/см^3, мы находим коэффициент d равным 6,9. Замечаем, что при таких уровнях индукции и частоты, потери на вихревые токи достигают до 99% от общих потерь для смеси -52. Остальные коэффициенты можно вычислить, основываясь на принципе наилучшего соответствия из данных, полученных при точных измерениях на низких частотах.
Еще одним аспектом модели Оливера является использование единого набора коэффициентов для всех возможных значений частоты и индукции в магнитном сердечнике.
Хотя эта модель была создана в первую очередь для распылённого железа, аналогичный подход можно применить и к другим магнитодиэлектрикам, таким как альсифер (KoolMu, SuperMSS), молипермаллой (MPP) и различные ферриты. В каждом случае нужно отдельно уточнять формулу для вычисления потерь на перемагничивание, чтобы обеспечить наилучшее соответствие характеристикам конкретного материала.

РЕКОМЕНДАЦИИ ДЛЯ Разработчиков ИМПУЛЬСНЫХ Источников ПИТАНИЯ
Температура окружающей среды ограничивает максимальный перегрев сердечника. Начальные расчёты следует проводить с одинаковыми значениями потерь как в обмотке, так и в сердечнике. Оптимально, чтобы потери в сердечнике были ниже потерь в обмотке, поскольку облегчить отвод тепла от обмотки проще, чем от сердечника.
На интернет-ресурсах доступны различные программы для расчёта индуктивных элементов (например, бесплатная программа от компании Micrometals [3]). Эти инструменты позволяют определить, на какой срок сердечник сможет безопасно функционировать в заданных условиях, принимая во внимание ранее упомянутое явление термического старения.
Если конструкция устройства предполагает использование вентилятора для теплоотведения, рекомендуется устанавливать вентилятор с фиксированной скоростью. В большинстве случаев потери в сердечнике не зависят от выходной мощности импульсного блока питания.
ЗАКЛЮчЕНИЕ
В течение последних нескольких десятилетий распылённое железо нашло широкое применение в радиоэлектронных устройствах как промышленного, так и бытового назначения. Чаще всего его используют для сердечников в дросселях, которые работают с большими токами смещения и подмагничивания, а также в дросселях электронных балластов для ламп дневного света, помехоподавляющих дросселях, дросселях для кассовых регистраторов и DC/DC-преобразователях, функционирующих в непрерывном режиме. Распылённое железо является самым недорогим порошковым материалом с высокой индукцией насыщения, что делает его использование во многих случаях более экономически выгодным по сравнению с молипермаллоем (МРР), альсифером (KoolMu, SuperMSS) или материалом HiFlux.
ЛИТЕРАТУРА
- Ridley R. and Nace A. Modeling Ferrite Core Losses. Switching Power Magazine. Winter 2002.
- Bozorth, Richard M. Ferromagnetism. Princeton: D. Van Nostrand, 1951.
- www.micrometals.com.